训练记录

• 倍增
  • $\color{#9D3DCF} \text{P4155 [SCOI2015]国旗计划}$
    • 开空间
    • 断环为链
    • 预处理
    • 验证可行性
• 堆
  • $\color{#3498DA} \text{P4053 [JSOI2007] 建筑抢修}$
    • 贪心策略
    • 直觉
• 数论分块
  • $\color{#F39C12} \text{P1403 [AHOI2005]约数研究}$
    • 法一
    • 法二
    • 双倍经验
  • $\color{#3498DA} \text{P2424 约数和}$
    • 数据范围
  • $\color{#3498DA} \text{P2261 [CQOI2007]余数求和}$
    • 二元关系
      • $n$ 与 $k$
      • $i$ 与 $k$
    • 数据范围
• 根号分块
  • $\color{#3498DA} \text{P3396 哈希冲突}$
    • 预处理
    • 查询
    • 修改

倍增

$\color{#9D3DCF} \text{P4155 [SCOI2015]国旗计划}$

环覆盖问题。

通过断环为链转化为线段覆盖问题。

对于一个战士 $i$，其后 $2^0$ 个士兵是固定的，即 $next = \max \{ j \vert D_i \ge C_j \}$。

倍增求出其后 $2^k$ 个士兵。

对于一次询问 $i$，倍增至 $C_i + M \lt D_j$。

将答案加上该士兵本身。

将答案加上用于奔袭在 $[C_i + M, D_j]$ 的士兵。

开空间

$maxN$ 要 $\times 2$。

$logN$ 要 $+ 1$。

int st[maxN * 2 + 10][logN + 1 + 10];

转移也是。

    for (int p = 1; p <= logN + 1; p++) for (int i = 1; i <= N * 2; i++) st[i][p] = st[st[i][p - 1]][p - 1];

断环为链

    for (int i = 1; i <= N; i++) {
        scanf("%lld%lld", &C[i], &D[i]);
        if (C[i] > D[i]) D[i] += M;
        soldier[i].id = i;
        soldier[i].l = C[i];
        soldier[i].r = D[i];
    }
    std::sort(soldier + 1, soldier + N + 1);
    for (int i = 1; i <= N; i++) {
        soldier[N + i].l = soldier[i].l + M;
        soldier[N + i].r = soldier[i].r + M;
    }

预处理

    int head = 0;
    for (int i = 1; i <= N * 2; i++) {
        while (head < N * 2 && soldier[head + 1].l <= soldier[i].r) head++;
        st[i][0] = head;
    }

验证可行性

$st_{now, p}$ 为空可不行。

   for (int i = 1; i <= N; i++) {
        int res = 2;
        int now = i;
        for (int p = logN + 1; p >= 0; p--) if (st[now][p] && soldier[st[now][p]].r < soldier[i].l + M) res += (1 << p), now = st[now][p];
        ans[soldier[i].id] = res;
    }

堆

$\color{#3498DA} \text{P4053 [JSOI2007] 建筑抢修}$

根据直觉按 $T_2$ 排序。

用 $T$ 记录已经花费的时间。

枚举每个建筑。

• 如果来得及：
  • 修理它并计数。
• 如果来不及：
  • 一定报废一栋建筑；
  • 考虑报废用时最长的建筑；
  • 在已经修理过的建筑中找到 $T_1$ 最大的建筑；
  • 若找到的 $T_1$ 比当前的 $T_1$ 大则进行替换：
    • 替换后 $S$ 不变；
    • 替换后 $T$ 减小，可用于修理更多建筑。

用堆维护已经修理过的 $T_1$。

    for (int i = 1; i <= N; i++) {
        T += Building[i].T1;
        Heap.push(Building[i].T1);
        if (T <= Building[i].T2) S++;
        else T -= Heap.top(), Heap.pop();
    }

贪心策略

仅仅按 $T_2$ 排序后贪心不一定是最优的，需要在中途进行转正。

$T_1$ 也是贪心策略的相关因素。

直觉

直觉是按 $dT = T_2 - T_1$ 排序。

即能修复该建筑的最晚开始时间。

错误原因同上。

更大的 $T_1$ 意味着更少的修复。

数论分块

$\color{#F39C12} \text{P1403 [AHOI2005]约数研究}$

\[\sigma(a) = \sum_{i \vert a} 1\]

求

\[\sum_{i = 1}^n \sigma(i)\]

法一

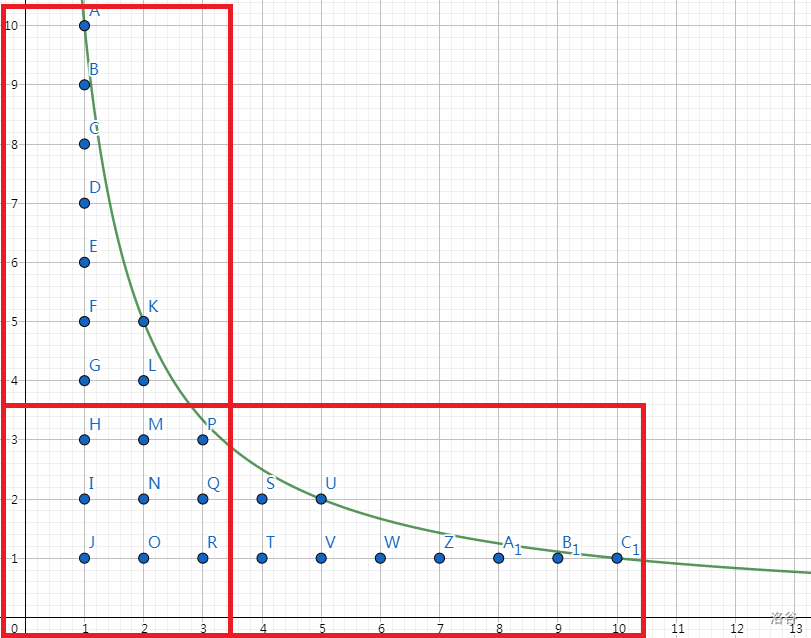
一目了然。

不言而喻。

枚举 $1$ 至 $sqrtN$。

$i$ 作为因数出现的次数为 $\lfloor \frac{n}{i} \rfloor$。

\[ans = \sum_{i - 1}^n \lfloor \frac{n}{i} \rfloor\]

int solve(int n) {
    int sqrtN = std::sqrt(n);
    int ret = 0;
    for (int i = 1; i <= sqrtN; i++) ret += n / i;
    return ret * 2 - m * m;
}

法二

打表发现：

对于一部分 $i$，$\lfloor \frac{n}{i} \rfloor$ 相同。

我们在 $\lfloor \frac{n}{i} \rfloor$ 首次出现时对其进行处理。

设 $\lfloor \frac{n}{i} \rfloor$ 相同的区间为 $[i, j]$。

\[j = \lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor} \rfloor\]

其贡献为：

\[\lfloor \frac{n}{i} \rfloor \cdot (j - i + 1)\]

int solve(int n) {
    int ret = 0;
    for (int i = 1, j, t; i <= n; i = j + 1) {
        t = n / i;
        j = n / t;
        ret += t * (j - i + 1);
    }
    return ret;
}

双倍经验

$\color{#3498DA} \text{P2424 约数和}$

\[\begin{aligned} \sigma(a) & = \sum_{i \vert a} 1 \\ f(a) & = \sum_{i \vert a} i \end{aligned}\]

仅贡献计算与上道题不同。

\[\begin{aligned} contribute_{last}(i, j) & = \lfloor \frac{n}{i} \rfloor \cdot (j - i + 1) \\ contribute_{this}(i, j) & = \lfloor \frac{n}{i} \rfloor \cdot \sum_{k = i}^j k \\ & = \lfloor \frac{n}{i} \rfloor \cdot (j - i + 1) \cdot \frac{i + j}{2} \end{aligned}\]

int solve(int n) {
    int ret = 0;
    for (int i = 1, j, t; i <= n; i = j + 1) {
        t = n / i;
        j = n / t;
        ret += t * (j - i + 1) * (i + j) / 2;
    }
    return ret;
}

数据范围

不开 $\text{long long}$ 见祖宗，只有 $10$ 分。

用于枚举的 $i$，$j$，$t$ 也要开，因为参与计算。

$\color{#3498DA} \text{P2261 [CQOI2007]余数求和}$

2022/11/15 $\color{#3498DA}蓝题$ $~50~$ $祭$

\[\begin{aligned} G(n, k) & = \sum_{i = 1}^{n} k \bmod i \\ & = \sum_{i = 1}^{n} k - i \lfloor \frac{k}{i} \rfloor \\ & = n k - \sum_{i = 1}^{n} i \lfloor \frac{k}{i} \rfloor \end{aligned}\]

int G(int n, int k) {
    int ret = n * k;
    for (int i = 1, j, t; i <= n; i = j + 1) {
        t = k / i;
        j = k / t;
        ret -= t * (j - l + 1) * (i + j) / 2;
    }
    return ret;
}

二元关系

$n$ 与 $k$

枚举的对象是 $n$，分块的对象是 $k$。计算 $\lfloor \frac{k}{i} \rfloor$ 和 $j$ 时不要把 $k$ 写成 $n$ 了。

当 $n \lt k$ 时，可能出现 $j > n$ 的情况，这并不在我们计算的范围内。

        j = std::min(n, k / t);

$i$ 与 $k$

我们知道，$t = \lfloor \frac{k}{i} \rfloor$ 表示 $i$ 作为 $k$ 的因数出现的次数。

当 $i \gt \frac{k}{2}$，$i$ 不是 $k$ 的因数，$t = 0$。

此时 $j = \lfloor \frac{k}{t} \rfloor$ 将无法计算，进行特判。

        t = k / i;
        if (t) j = std::min(n, k /t);
        else j = n;

数据范围

根据

\[G(n, k) = n k - \sum_{i = 1}^{n} i \lfloor \frac{k}{i} \rfloor\]

可知，$n$，$k$ 也直接参与答案的计算，故需要开 $\text{long long}$。

综上：

long long G(long long n, long long k) {
    long long ret = n * k;
    for (long long i = 1, j, t; i <= n; i = j + 1) {
        t = k / i;
        if (t) j = std::min(n, k / t);
        else j = n;
        ret -= t * (j - i + 1) * (i + j) / 2;
    }
    return ret;
}

根号分块

$\color{#3498DA} \text{P3396 哈希冲突}$

int Query(int x, int y) {
    int ret = 0;
    for (int i = y; i <= n; i++) ret += x;
    return ret;
}

查询复杂度为 $\mathcal{O}(n^2)$。

令 $block[x][y]$ 表示模数为 $x$ 余数为 $y$ 时的答案。

void PreWork() {
    for (int i = 1; i <= n; i++) {
        for (int x = 1; x <= n; x++) {
            int y = i % x;
            block[x][y] += value[i];
        }
    }
    return;
}

预处理复杂度为 $\mathcal{O}(n^2)$。

空间复杂度为 $\mathcal{O}(n^2)$。

• 对模数 $x$ 进行分块；
• 当模数 $x$ 小于 $sqrtN$ 时：预处理；
• 当模数 $x$ 大于 $sqrtN$ 时：暴力。

预处理

void PreWork() {
    for (int i = 1; i <= sqrtN; i++) {
        for (int x = 1; x <= n; x++) {
            int y = i % x;
            block[x][y] += value[i];
        }
    }
    return;
}

预处理复杂度降为 $\mathcal{O}(n \sqrt n)$。

空间复杂度降为$\mathcal{O}(n)$。

查询

int Query(int x, int y) {
    if (x <= sqrtN) return block[x][y];
    int ret = 0;
    for (int i = y; i <= n; i += x) ret += value[i];
    return ret;
}

查询复杂度分别为 $\mathcal{O}(1)$，$\mathcal{O}(\sqrt n)$。

修改

void Modify(int x, int y) {
    for (int i = 1; i <= sqrtN; i++) {
        block[i][x % i] += y - value[x];
    }
    value[x] = y;
    return;
}

修改复杂度为 $\mathcal{O}(\sqrt n)$。